今天是讲的也是微分方程最难的部分,二阶常系数线性微分方程,当然说它难,也是纸老虎,因为“一个萝卜一个坑”,每类题型都有固定的套路。
二阶常系数线性微分方程,有齐次和非齐次两种,而且非齐次通解的解法包含齐次的,因此先讲齐次,后讲非齐次。
问题索引:
- 二阶常系数齐次线性微分方程的解题流程是什么?
- 二阶常系数非齐次线性微分方程的解题流程是什么?
先讲齐次的,直接拿例题来说吧:
例:
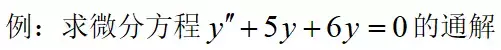
第一步:写出特征方程,需要注意特征方程和原方程的对应关系

解得
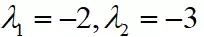
第二步:写出通解
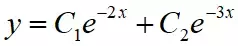
一般来说通解就这么写,两个e脑袋上x的系数分别对应两个特征根,当然,特征根可不一定存在,因此得分成几种情况进行讨论。
如果解出来的是两个不同的实根,则通解形式为:
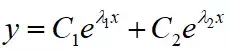
如果解出来是两个相同的实根,则通解形式为:

如果解出来是两个共轭复根,则通解形式为:
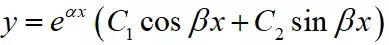
这样的话齐次就讲完了,基本程序就是解一个一元二次方程,然后根据解的情况写对应的通解形式。
下面就是非齐次的求解:
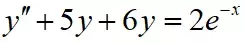
第一步先求对应齐次的通解,这个已经求过了,下面就是求非齐次的一个特解,方法就是待定系数法,待定系数法比较复杂,请认真看我的操作:
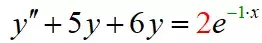
设:
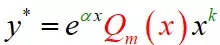
看到颜色的不同了吧,首先看红色,原方程是2,是一个0次多项式,因此设出来的函数就是一个常数A,红色部分的对应关系就是次数相同,比如原方程红色部分是一个二次多项式,那么设出来的函数也是二次的,二次的就是三个待定系数。
再来看绿色部分,原方程是-1,跟两个求出来的特征根-2,-3都不一样,因此立即推k=0
如果原方程是-2呢,说明跟特征根对上了,那么k=1
如果原方程的特征根-2是一个二重根,而原方程绿色部分也是-2,跟这个二重根对上了,那么k=2
所以,最终的结果是,
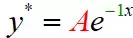
代入求解即可。
答案:
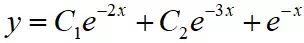
思考题:
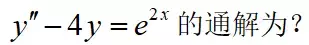
答案:
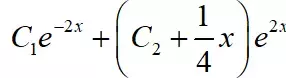
恭喜你,又学会了一个知识点。
